Rombun sahəsini hesablamağın 3 yolu

2024 Müəllif: Jason Gerald | [email protected]. Son dəyişdirildi: 2023-12-16 10:54

Bir romb, dörd bərabər tərəfi olan dördküncdür. Bir rombun sahəsini tapmaq üçün üç düstur var. Necə olduğunu bilmək üçün sadəcə bu addımları izləyin.

Addım

Metod 1 /3: diaqonal istifadə

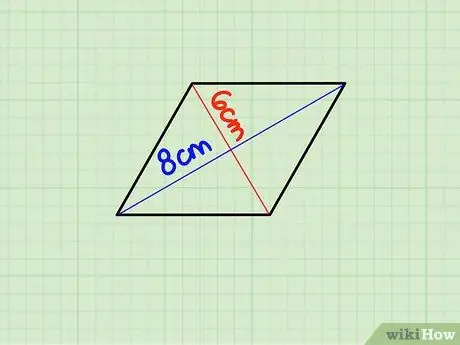
Addım 1. Hər bir diaqonalın uzunluğunu tapın

Bir rombun diaqonalları, formanın mərkəzində əks təpələri (küncləri) birləşdirən xətlərdir. Bir rombun diaqonalları dikdir və kəsişmə nöqtəsi boyunca dörd düzbucaqlı üçbucaq təşkil edir.

Diaqonalın 6 sm, uzunluğunun 8 sm olduğunu düşünək

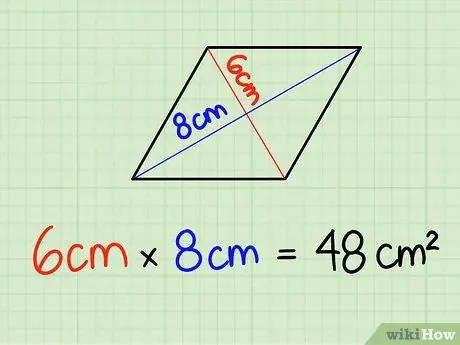
Addım 2. Diaqonalın uzunluğunu vurun

Yalnız diaqonalın uzunluğunu yazın və vurun. Bu vəziyyətdə 6 sm x 8 sm = 48 sm². Vahidləri çoxaltmağı unutmayın, çünki kvadrat vahidlərlə işləyirik.

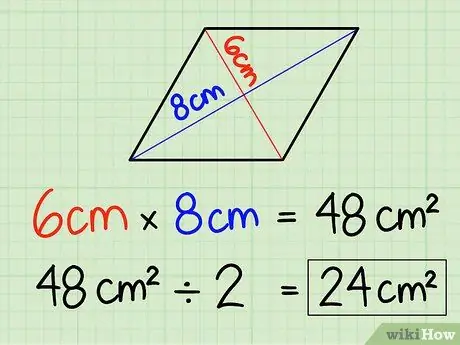
Addım 3. Nəticəni 2 -yə bölün

Çünki 6 sm x 8 sm = 48 sm², nəticəni 2.48 sm -ə bölmək kifayətdir²/2 = 24 sm². Bir rombun sahəsi 24 sm -dir².

Metod 2 /3: Baza və Boydan istifadə

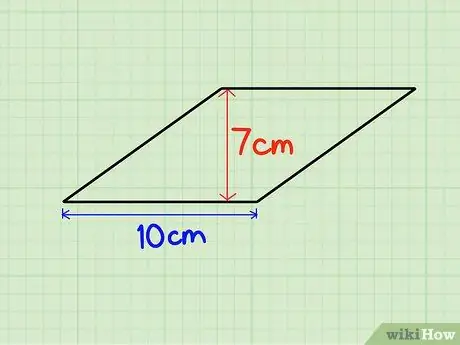
Addım 1. Baza və hündürlüyü tapın

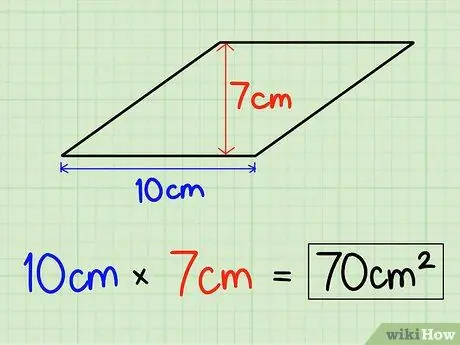
Rombun hündürlüyünü rombun yan tərəfinin uzunluğuna vura bilərik. Deyək ki, rombun hündürlüyü 7 sm, əsası isə 10 sm -dir.

Addım 2. Baza və hündürlüyü vurun

Rombun əsasını və hündürlüyünü bildikdən sonra, çarpmaqla formanın sahəsini tapın. Beləliklə, 10 sm x 7 sm = 70 sm². Bir rombun sahəsi 70 sm -dir².

Metod 3 /3: Trigonometriyadan istifadə

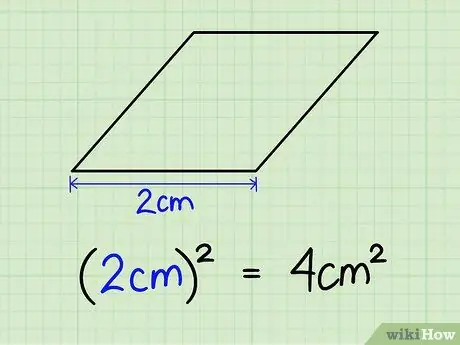
Addım 1. İstənilən tərəfin uzunluğunu kvadrat edin

Bir rombun dörd bərabər tərəfi var, buna görə də hansı tərəfi seçməyimizin əhəmiyyəti yoxdur. Tutaq ki, tərəfin uzunluğu 2 sm -dir. 2 sm x 2 sm = 4 sm².

Addım 2. Bir küncün sinusu ilə vurun

Hansı bucağı seçməyimizin əhəmiyyəti yoxdur. Deyək ki, açılardan biri 33 dərəcədir. Sinusu (33) 4 sm -ə vurmaq kifayətdir² romb sahəsini əldə etmək. (2 sm)² x sinus (33) = 4 sm² x 1 = 4 sm². Bir rombun sahəsi 4 sm -dir².