Digər iki bucağın ölçüsünü bildiyiniz müddətcə üçbucağın üçüncü bucağını tapmaq asandır. İki açının cəmini 180 dərəcə çıxarmaq kifayətdir. Bununla birlikdə, problemin forması adi haldan bir az fərqli olarsa, üçbucağın üçüncü bucağını tapmaq üçün istifadə edə biləcəyiniz başqa yollar da var. Üçbucağın üçüncü bucağını necə tapacağınızı bilmək istəyirsinizsə, aşağıdakı təlimatı izləyin.
Addım
Metod 3: Digər İki Bucağın Ölçülərindən istifadə
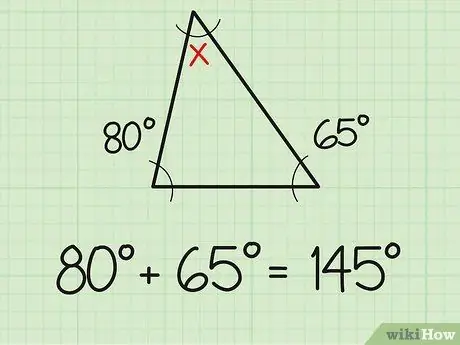
Addım 1. İki məlum bucağı əlavə edin
Bilməli olduğunuz bir həqiqət budur ki, üçbucağın üç bucağının cəmi həmişə 180 dərəcədir. Beləliklə, üçbucağın iki bucağının ölçüsünü artıq bilirsinizsə, üçüncü bucağı tapmaq sadə toplama və çıxma problemləri etmək qədər sadə olacaq. Əvvəlcə bildiyiniz iki bucaq ölçüsünü əlavə edin. Məsələn, iki məlum bucaq 80 və 65 dərəcə ölçülür. İkisini birlikdə əlavə edin (80+65) və 145 dərəcə əldə edin.
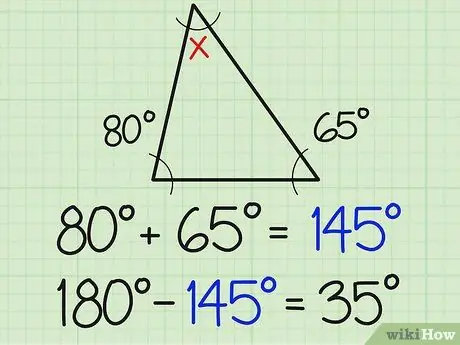
Addım 2. Bu rəqəmi 180 -ə bölün
Üçbucağın üç bucağının cəmi həmişə 180 dərəcədir. Buna görə də, bucağın bilinən iki ölçüsünün cəminə əlavə edildikdə üçüncü bucaq 180 olmalıdır. Yuxarıdakı nümunədə bu 180-154 = 35 deməkdir.
Addım 3. Cavabınızı yazın
İndi üçüncü bucağa cavabınız var (nümunədə 35 dərəcə). Hələ də şübhəniz varsa, özünüz baxın. Üç bucağı birlikdə əlavə edin və 180 nəticə əldə etməlisiniz. Əks təqdirdə hesablamanız səhvdir. Bu nümunə üçün 80+65+35 = 180. Düzgündürsə, bu, problemi həll etdiyiniz deməkdir.
Metod 2 /3: Dəyişənlərdən istifadə
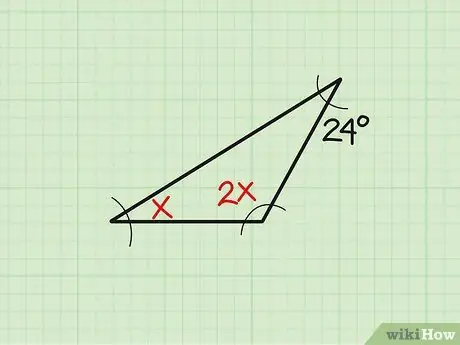
Addım 1. Problemi yazın
Bəzən mövcud bucağın ölçüsü dəyişkən formada göstərilir. Bu nümunəni götürək: "Üç bucaq sırasıyla" x "," 2x "və 24 ölçürsə, üçbucağın" x "açısını tapın." Əvvəlcə problemi yazın.
Addım 2. Bütün bucaq ölçülərini əlavə edin
Xatırlamalı olduğunuz prinsip eyni olaraq qalır. Beləliklə, əvvəlcə problemdəki üç bucağı toplayın, yəni "x+2x+24 = 3x+24".
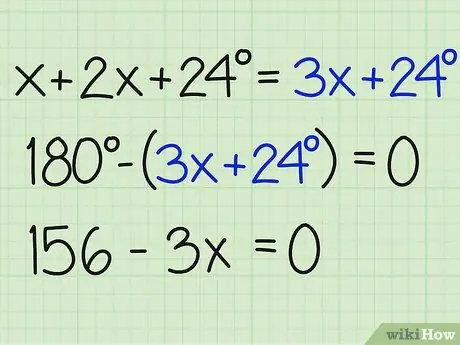
Addım 3. Bucaqların cəmini 180 -ə bölün
İndi x -i tapmaq və problemin cavabını tapmaq üçün bu rəqəmi 180 dərəcə fərqləndir. Tənliyi sıfıra bərabər bitirdiyinizə əmin olun. Budur necə yazılır:
- 180- (3x+24) = 0
- 180-3x-24 = 0
- 156-3x = 0
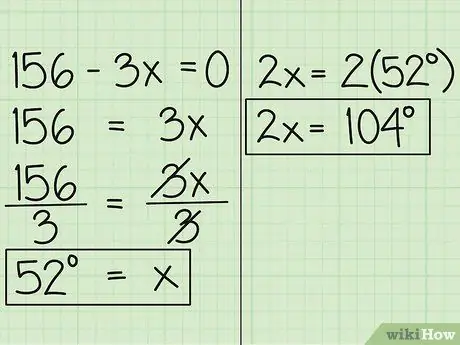
Addım 4. x -in dəyərini tapın
İndi dəyişəni tənliyin digər tərəfinə aparın, 156 = 3x alacaqsınız. Sonra tənliyi 3 -ə bölün, beləliklə x = 52 alacaqsınız. Bu, x ilə ifadə olunan bucağın ölçüsünün 52 dərəcə olduğu deməkdir. 2x ilə ifadə olunan digər bucaq, 52 dərəcə 2, yəni 104 dərəcədir.
Addım 5. Nəticələrinizi yoxlayın
Cavabınızın düzgün olduğundan əmin olmaq istəyirsinizsə, cavabını tapdığınız üç bucaq ölçüsünü əlavə edin. Nəticə 180 -dirsə, bu cavabınızın doğru olduğunu göstərir. Bu nümunə üçün 52+104+24 = 180.
Metod 3 /3: Digər metodlardan istifadə
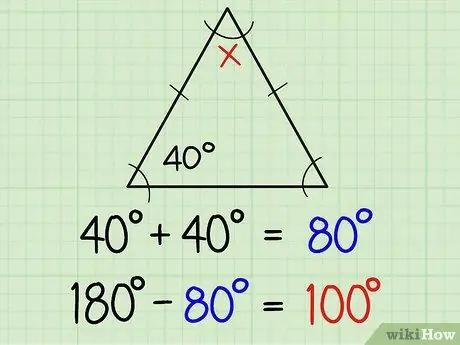
Addım 1. İki tərəfli üçbucağın açılarını tapın
İki tərəfli üçbucağın iki bərabər tərəfi və iki bərabər açısı var. İki bərabər tərəf ümumiyyətlə yan xəttin ortasında kiçik bir xətt ilə işarələnir, yəni xəttin iki əks açısı eyni ölçüdür. Bir bucağın ölçüsünü artıq bilirsinizsə, avtomatik olaraq digər bucağı da tanıyırsınız. Əlavə izahat budur:
Bərabər açılardan biri 40 dərəcədirsə, digəri 40 dərəcədir. Bu şəkildə 40+40 (yəni 80) ilə 180 və ya başqa sözlə 180-80 = 100 arasındakı fərqlə hər üç açını tapa bilərsiniz
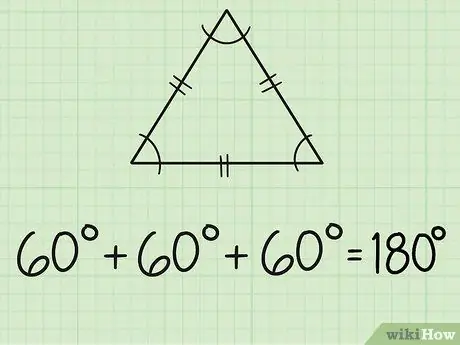
Addım 2. Bərabər tərəfli üçbucağın açılarını tapın
Bərabər üçbucağın üç bərabər tərəfi və üç bərabər açısı var. Hər tərəf ümumiyyətlə ortada iki qısa xətt ilə qeyd olunur. Hər üç bucaq bərabər olduğu üçün bütün açılar 60 dərəcə ölçülür, çünki 180/3 = 60.
Addım 3. Düzbucaqlı üçbucağın üçüncü bucağını tapın
Tutaq ki, kəskin bucaqlardan biri 30 dərəcə olan bir düzbucaqlı üçbucaq əldə edirsiniz. Üçbucaq düz bucaq olduğundan, bucaqlardan birinin, yəni düz bucağın 90 dərəcə ölçülməsi lazımdır. Sonra üçbucaq prinsipini istifadə edin, iki bucağın cəmi arasındakı fərq (90+30 = 120) 180, onda 180-120 = 60 dərəcə alacaqsınız.
