- Müəllif Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:09.
- Son dəyişdirildi 2025-01-23 12:06.
Statistikada, rejim ən çox rəqəm və ya məlumat toplusunda görünən rəqəmdir. məlumatların özündə həmişə yalnız bir rejim yoxdur, iki və ya daha çox ola bilər (buna görə də bimodal və ya multimodal deyilir). Başqa sözlə, bir məlumatda ən çox rast gəlinən bütün ədədlər rejim adlandırıla bilər. Rejimi necə tapacağınızı öyrənmək üçün aşağıdakı addımları izləyin.
Addım
Metod 1 /2: Məlumat Modunu Tapın

Addım 1. Məlumatdakı nömrələri yazın
Rejim ümumiyyətlə statistik məlumatlardan və ya rəqəmlər siyahısından götürülür. Buna görə rejimi tapmaq üçün məlumatlara ehtiyacınız var. Əvvəlcə məlumatları qeyd etməyiniz və ya yazmağınız məsləhət görülür, çünki çox az olduğu təqdirdə yalnız ağlınızda görüb təhlil edərək rejimi tapmaq olduqca çətindir. Kağız və qələm və ya qələmdən istifadə edirsinizsə, daha sonra sıralamaq üçün əvvəlcə məlumatları yazın. Bir kompüterdəsinizsə, onları sonradan avtomatik olaraq sıralamaq üçün elektron tablo proqramından istifadə edə bilərsiniz.
Bir nümunə problemindən istifadə etsək, bir məlumat rejimini tapmaq prosesini başa düşmək daha asandır. Hələlik bu nümunə məlumatlardan istifadə edək: {18, 21, 11, 21, 15, 19, 17, 21, 17}. Növbəti bir neçə addımda rejimi kəşf edəcəyik.

Addım 2. Nömrələri kiçikdən böyüyə qədər sıralayın
Məlumatların çeşidlənməsi əslində edilə bilməz. Ancaq bu addım rejimi tapmaqda həqiqətən kömək edəcək, çünki eyni ədədlər bir -birinin yanında olacaq və hesablamanı asanlaşdıracaq. Məlumatlarınızın ölçüsü çox böyükdürsə, xətaya meylli olma nisbətini azaltmaq üçün bu addım atılmalıdır.
- Kağız və qələm və ya qələm istifadə edirsinizsə, əvvəllər yazdığınız məlumatları sırayla yenidən yazın. Verilərdən ən kiçik rəqəmi taparaq başlayın. Taparsanız, yeni bir sətrə yazın, sonra əvvəlki məlumatlar siyahısındakı nömrəni silin. Növbəti ən kiçik nömrəni tapın və bütün nömrələri sıralayana qədər eyni şeyi edin.
- Kompüterinizdə bir elektron tablo proqramı istifadə edirsinizsə, nömrələrin siyahısını bir neçə kliklə sıralaya bilərsiniz.
-
Yuxarıdakı nümunəmizdə sıralanan məlumatlar belədir {11, 15, 17, 17, 18, 19, 21, 21, 21}.

Nömrələr Dəstinin Modunu Tapın Adım 3 Addım 3. Bir ədədin neçə dəfə göründüyünü sayın
Kiçik məlumatlar üçün sıralanan məlumatlara baxa bilərsiniz, sonra orada ən çox görünən rəqəmi axtara bilərsiniz. Veriləriniz daha böyükdürsə, səhvlərin qarşısını almaq üçün onları bir -bir hesablamalısınız.
- Kağız və qələm və ya qələm istifadə edirsinizsə, səhv hesablamaların qarşısını almaq üçün hər ədədin neçə dəfə göründüyünə diqqət yetirin. Bir kompüterdə bir cədvəl istifadə edirsinizsə, onu başqa bir sütuna da yaza bilərsiniz və ya bilirsinizsə, proqramda verilən düsturlardan istifadə edə bilərsiniz.
- Misal problemində, yəni ({11, 15, 17, 17, 18, 19, 21, 21, 21}), 11 sayı bir dəfə, 15 bir dəfə, 17 iki dəfə, 18 bir dəfə, 19 bir dəfə, və 21 üç dəfə görünür. Oradan aydın olur ki, 21 ən çox görünən rəqəmdir.

Nömrələr toplusunun rejimini tapın Adım 4 Addım 4. Ən çox görünən nömrə məlumatların rejimidir
Eyni nömrələrin hər birinin neçə dəfə göründüyünü qeyd etdikdən sonra artıq bilməlisiniz ən çox hansı rəqəm görünür, bu da məlumat rejimi deməkdir. Bunu yadda saxla bir məlumatın birdən çox rejimi olması mümkündür. Bir məlumatın iki rejimi varsa, məlumatlara bimodal, üç rejimə sahibsə trimodal və s.
- Misal problemində, rejimi 21 -dir çünki ən çox görülür.
- Üç dəfə görünən başqa bir nömrə varsa, 21 və bu nömrə rejimdir.

Nömrələr toplusunun rejimini tapın 5 -ci addım Addım 5. Məlumat rejimini orta (orta) və medianaya görə fərqləndirin
Üç statistik anlayış ümumiyyətlə bir müzakirədə müzakirə olunur. Adları oxşar olduqları və bəzən eyni dəyərə sahib olduqları üçün bir çox insanlar onları ayırmaqda çətinlik çəkirlər. Bununla birlikdə, məlumatların eyni rejimi, medianı və ya ortalaması olsa da, fərqli olduqlarını və tək qaldıqlarını unutmayın. Aşağıdakı izahı oxuyun.
-
Ortalama mənasını verən orta məlumat dəyərlərinin məlumat sayına bölünməsidir. Məsələn, nümunə problemində ({11, 15, 17, 17, 18, 19, 21, 21, 21}), ümumi məlumatlar 11 + 15 + 17 + 17 + 18 + 19 + 21 + 21 + 21 = 160. Verilərdə 9 dəyər olduğu üçün 160/9 = 17.78.

Nömrələr Dəstinin Modunu Tapın Adım 5Bullet1 -
Median, məlumatların sıralanmasından sonra orta dəyərdir və kiçik və böyük dəyərləri məlumatlardan ayırır. Misal problemində ({11, 15, 17, 17, 18, 19, 21, 21, 21}) median
Addım 18. çünki nömrə ortadadır və məlumatlarda 18 -dən aşağı olan dörd ədəd yüksək və dörd ədəd aşağıdır. Verilər cüt rəqəmdirsə, ortada iki ədədin cəminin hesablanması və sonra ikiyə bölünməsi ilə median əldə edilir.

Nömrələr Dəstinin Modunu Tapın Adım 5Bullet2
Metod 2 /2: Xüsusi bir problemdə rejimi tapmaq

Nömrələr toplusunun rejimini tapın Adım 6 Addım 1. Veridəki bütün ədədlər eyni sayda hadisəyə sahib olduqda məlumatın rejimi yoxdur
Məsələn, bütün ədədlər yalnız bir dəfə görünsə, məlumatlar rejimi yoxdur çünki heç bir rəqəm digərindən daha tez -tez görünmür. Bütün nömrələr iki dəfə və ya daha çox görünsə də eyni şeydir.
Yuxarıdakı nümunə problemindəki məlumatları {11, 15, 17, 18, 19, 21} olaraq dəyişdirsək, bu, bütün ədədlərin bir dəfə göründüyü deməkdir, onda məlumatların rejimi yoxdur, həmçinin məlumatlar {11 olaraq dəyişdirilərsə, 11, 15, 15, 17, 17, 18, 18, 19, 19, 21, 21}

Nömrələr dəstinin rejimini tapın Adım 7 Addım 2. Rəqəmsal olmayan məlumatlar hələ də rəqəmsal məlumatlar kimi onun rejimi üçün axtarıla bilər
Adətən məlumatlar kəmiyyət və ya ədədi formada mövcuddur, buna görə də bir çox üsulla işlənə bilər. Ancaq bəzən rəqəm şəklində olmayan şeylər var. Bununla birlikdə, bu məlumat rejimi hələ də ən çox rast gəlinən məlumatları (ifadələr şəklində ola bilər) axtararaq axtarıla bilər. Ancaq ədədi olmayan məlumatların ortalamasını və ya medianını tapa bilməzsiniz.
- Məsələn, ərazinizdə hansı ağac növlərinin böyüdüyünü öyrənmək üçün bioloji bir araşdırma apardığınızı düşünün. Aldığınız məlumatlar {Fire, Mango, Spruce, Palm, Spruce, Fir, Mango, Mango, Palm, Fir}. Bu cür məlumatlar nominal məlumatlar adlanır, çünki hər bir məlumat dəyəri bir adla fərqlənir. Bu nümunə üçün rejim belədir küknar çünki ən çox (beş dəfə) görünür.
- Nümunəyə baxsanız, ortalamanı və ya medianı hesablamağın heç bir yolu yoxdur.
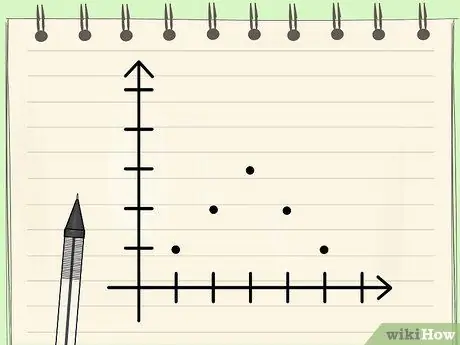
Nömrələr toplusunun rejimini tapın Adım 8 Addım 3. Bilin ki, simmetrik olmayan unimodal məlumat paylanması üçün məlumatların rejimi, medianası və ortalaması eyni olacaq
Daha əvvəl qeyd edildiyi kimi, bir məlumat dəstinin ortalaması, medianası və rejimi eyni olduğu zamanlar olacaq. Şərtlərdən biri, məlumatların ciddi şəkildə simmetrik olaraq paylanmasına malik olmasıdır (qrafik formada çəkilərsə Gauss zənginə bənzər bir əyri meydana gətirər). Dağıtım simmetrik olduğundan, bu kimi məlumatların rejimi avtomatik olaraq ortada olan məlumatlardır, çünki ən çox görünən məlumatlar olmalıdır və orta dəyər olduğu üçün bu rəqəmin də orta olduğunu göstərir.. Riyazi hesablamalar aparsanız, ortalamalar eyni rəqəmi verəcəkdir.
- Məsələn, {1, 2, 2, 3, 3, 3, 4, 4, 5} məlumatlarından, qrafiki çəksəniz, parabola qrafiki alacaqsınız. Məlumat rejimi 3 -dir ən çox göründüyü üçün median 3 -dir çünki sayı ortada və ortalaması 1 + 2 + 2 + 3 + 3 + 3 + 4 + 4 + 5 = 27/9 = 3.
- Bu kimi halların istisnaları var, yəni bu simmetrik məlumatların birdən çox rejimi olduqda. Əgər belədirsə, orta və median birdən çox dəyər ola bilmədiyi üçün bu rejim orta və orta ilə eyni olmayacaq.
İpuçları
- Məlumatların birdən çox rejimi ola bilər
- Məlumatdakı bütün ədədlərin baş vermə sayı eyni olarsa, məlumat rejimi mövcud deyil.






